Plackett-Luce Trees

Recursive partitioning based on Plackett-Luce models.

Usage

pltree(formula, data, worth, na.action, cluster, ref = NULL, ...)

Arguments

formula

A symbolic description of the model to be fitted, of the form y ~ x1 + ... + xn where y should be an object of class grouped_rankings and x1, ..., xn are used as partitioning variables.

data

An optional data object containing the variables in the model. Either a data frame of variables in formula or a list of length 2 giving data frames for variables in formula and in worth.

worth

A optional formula specifying a linear model for log-worth. If NULL, worth is estimated separately for each item with PlackettLuce(). Otherwise, the model in each node of the tree id fitted with pladmm().

na.action

how NAs are treated for variables in formula, applied to the underlying rankings.

cluster

an optional vector of cluster IDs to be employed for clustered covariances in the parameter stability tests, see mob.

ref

an integer or character string specifying the reference item (for which log ability will be set to zero). If NULL the first item is used.

...

additional arguments, passed to PlackettLuce of pladmm().

Value

An object of class "pltree" inheriting from "bttree"

and "modelparty".

Details

Plackett-Luce trees are an application of model-based recursive partitioning (implemented in mob) to Plackett-Luce models for rankings. The partitioning is based on ranking covariates, e.g. attributes of the judge making the ranking, or conditions under which the ranking is made. The response should be a grouped_rankings object that groups rankings with common covariate values. This may be included in a data frame alongside the covariates.

Most arguments of PlackettLuce can be passed on by pltree. However, Plackett-Luce tree with fixed adherence are not implemented. Arguably it makes more sense to estimate adherence or reliability within the nodes of the Plackett-Luce tree.

Various methods are provided for "pltree" objects, most of them inherited from "modelparty" objects (e.g. print, summary), or "bttree" objects (plot). The plot method employs the node_btplot panel-generating function. The See Also section gives details of separately documented methods.

See also

bttree For fitting Bradley-Terry trees (equivalent to the Plackett-Luce model for paired comparisons without ties).

coef, vcov, AIC and predict methods are documented on pltree-summaries.

itempar, extracts the abilities or item parameters in each node of the tree using itempar.PlackettLuce.

fitted, computes probabilities for the observed choices based on the full tree.

Examples

# Bradley-Terry example

if (require(psychotree)){
    ## Germany's Next Topmodel 2007 data
    data("Topmodel2007", package = "psychotree")
    ## convert paircomp object to grouped rankings
    R <- as.grouped_rankings(Topmodel2007$preference)
    ## rankings are grouped by judge
    print(R[1:2,], max = 4)
    ## Topmodel2007[, -1] gives covariate values for each judge
    print(Topmodel2007[1:2, -1])

    ## fit partition model based on all variables except preference
    ## set npseudo = 0 as all judges rank all models
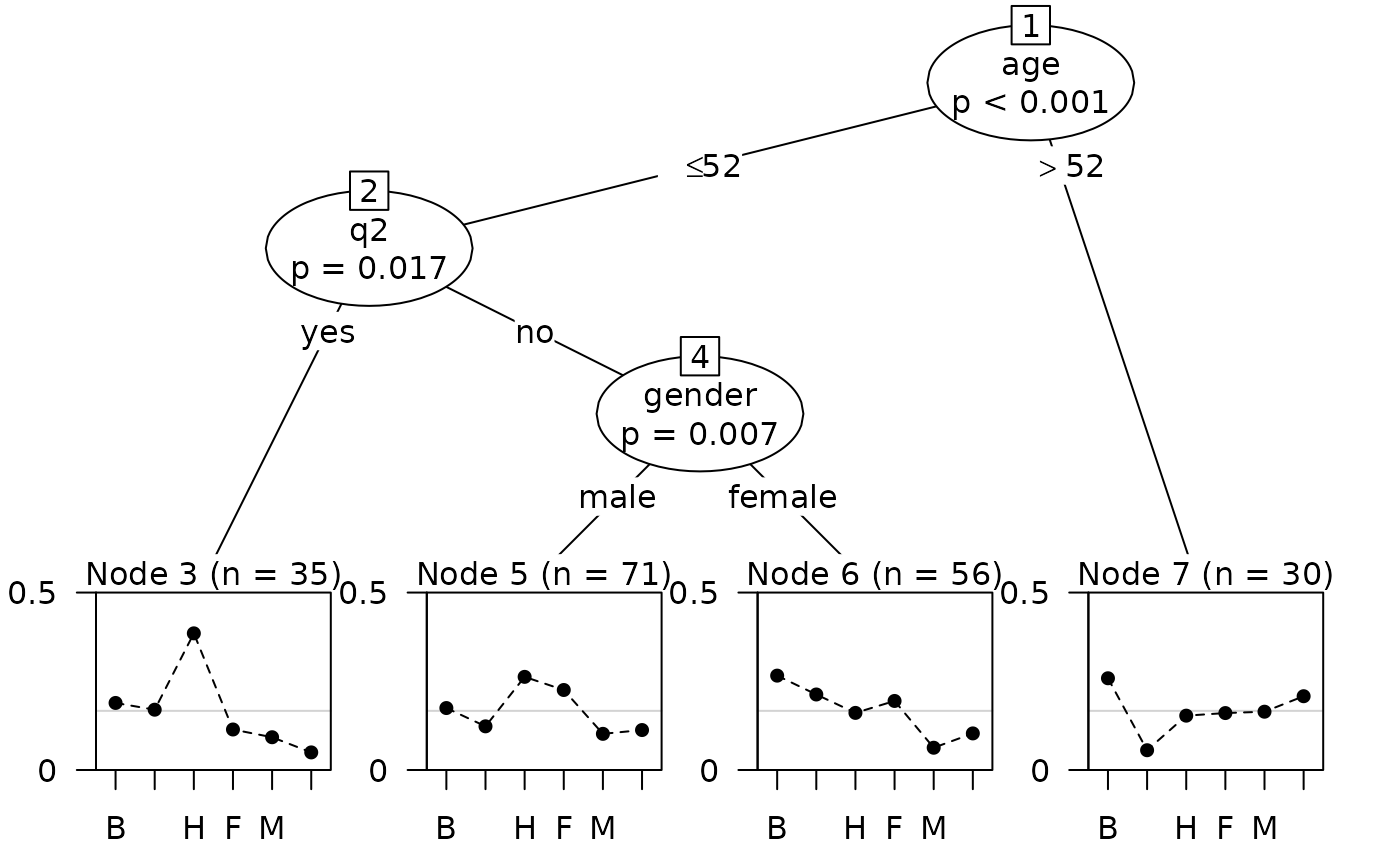
    tm_tree <- pltree(R ~ ., data = Topmodel2007[, -1], minsize = 5,
                      npseudo = 0)

    ## plot shows abilities constrained to sum to 1
    plot(tm_tree, abbreviate = 1, yscale = c(0, 0.5))
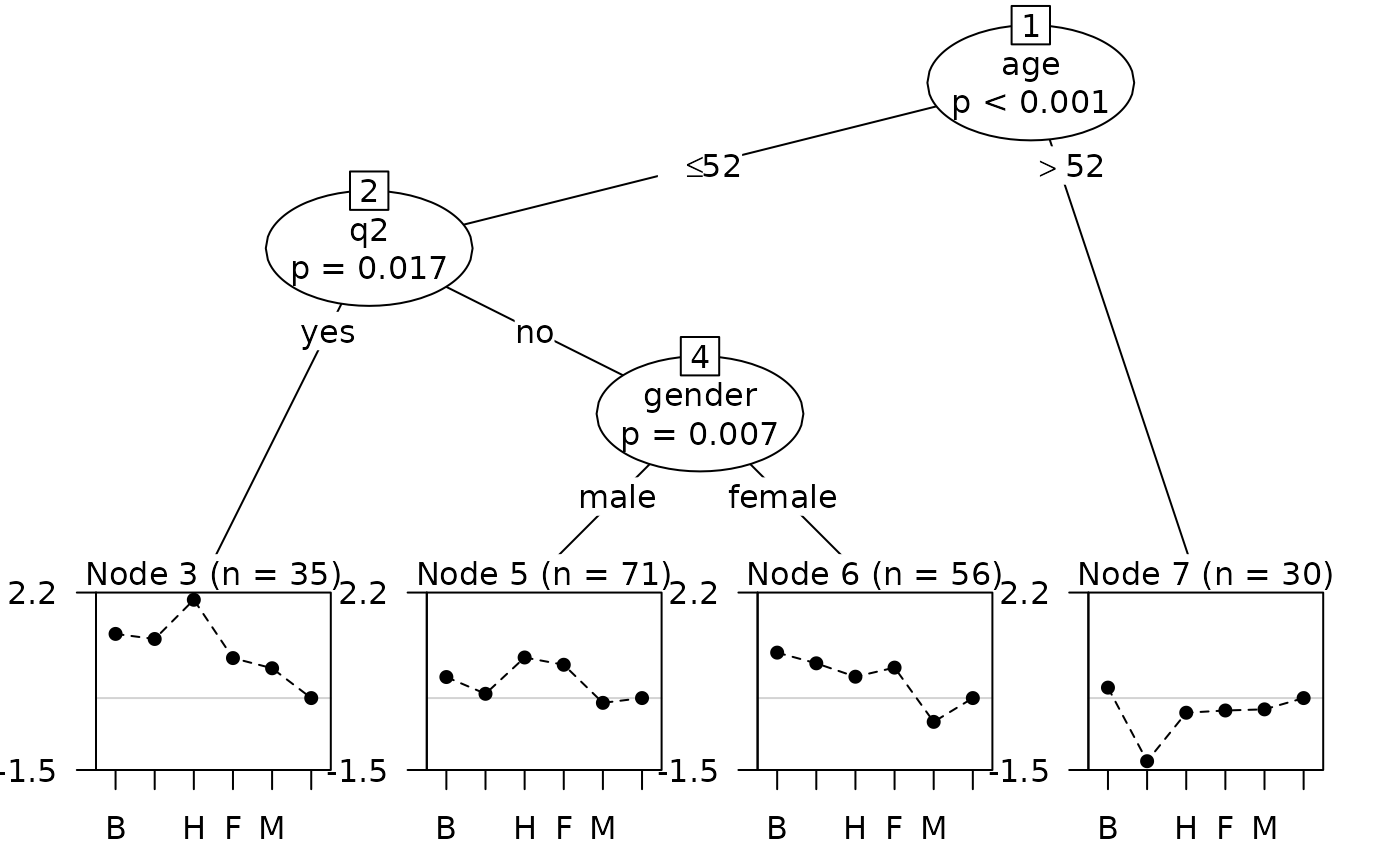
    ## instead show log-abilities with Anja as reference (need to used index)
    plot(tm_tree, abbreviate = 1, worth = FALSE, ref = 6,
         yscale = c(-1.5, 2.2))

    ## log-abilities, zero sum contrast
    itempar(tm_tree, log = TRUE)
}
#> Loading required package: psychotree
#> Loading required package: partykit
#> Loading required package: grid
#> Loading required package: libcoin
#> Loading required package: mvtnorm
#> 
#> Attaching package: ‘mvtnorm’
#> The following object is masked from ‘package:gnm’:
#> 
#>     Mult
#> Loading required package: psychotools
#>                                                                   1 
#> "Barbara > Anni, Barbara > Hana, Anni > Hana, Barbara > Fiona, ..." 
#>                                                                   2 
#> "Anni > Barbara, Hana > Barbara, Hana > Anni, Fiona > Barbara, ..." 
#>   gender age  q1  q2  q3
#> 1   male  66  no  no  no
#> 2   male  21 yes yes yes


#>     Barbara       Anni       Hana      Fiona       Mandy       Anja
#> 3 0.3252815  0.2193055 1.03734300 -0.1785927 -0.39080852 -1.0125288
#> 5 0.1106734 -0.2392155 0.51830152  0.3662483 -0.42801793 -0.3279899
#> 6 0.5715647  0.3486194 0.06927133  0.2590188 -0.87250735 -0.3759669
#> 7 0.5343475 -1.0000476 0.01067104  0.0575107  0.08093274  0.3165856